方法递归调用
基本介绍
简单地说:递归就是方法自己调用自己,每次调用时传入不同的变量.递归有助于编程者解决复杂问题,同时可以让代码变的简洁
递归能解决什么问题
- 各种数学问题如:8皇后问题,汉诺塔,阶乘问题,迷宫问题,球和篮子的问题
- 各种算法也会使用到递归,比如快排,归并排序,二分查找,分治算法等
- 将用栈解决的问题–>递归代码比较简洁
递归举例
列举两个小案例,来理解递归调用机制
- 打印问题
- 阶乘问题
public class Recursion01 {
public static void main(String[] args) {
// TODO Auto-generated method stub
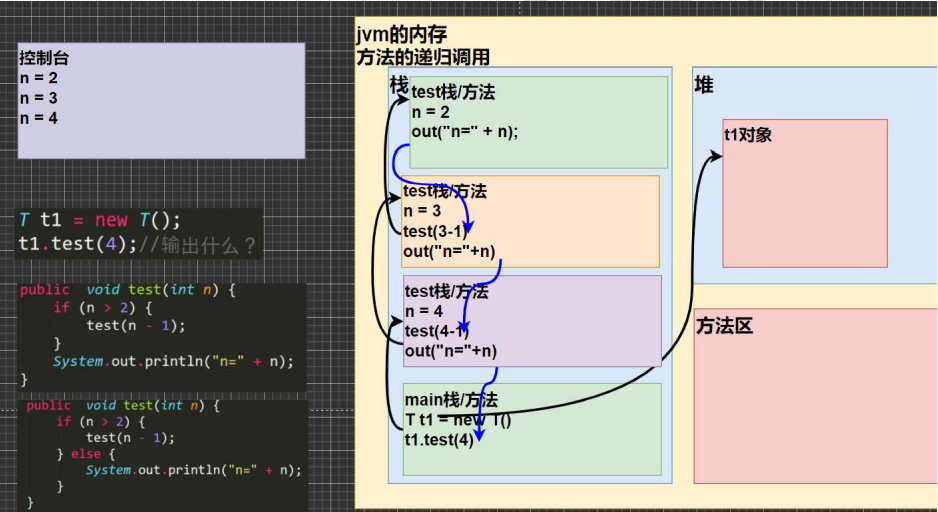
T t1=new T();
t1.test(4);//输出n=2 n=n3 n=4
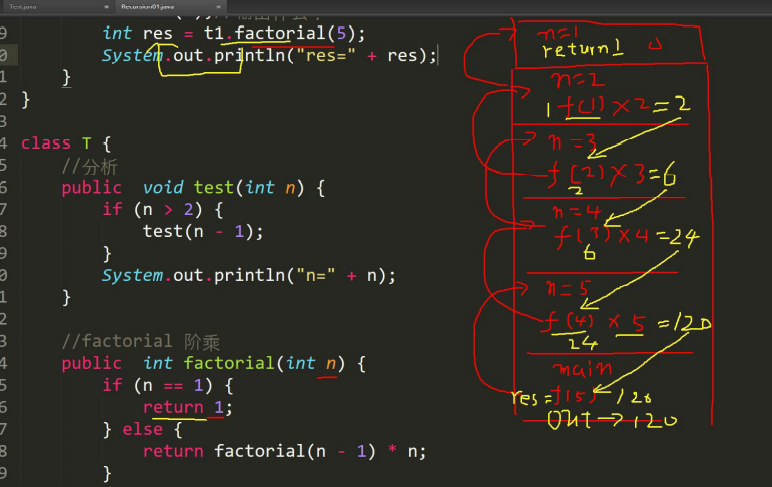
int res= t1.factorial(5);
System.out.println("5的阶乘的结果="+res);
}
}
class T{
//分析
public void test(int n) {
if(n>2) {
test(n-1);
}
System.out.println("n="+n);
}
//factorial阶乘
public int factorial(int n) {
if(n==1) {
return 1;
}else {
return factorial(n-1)*n;
}
}
}
递归重要原则
- 执行一个方法时,就创建一个新的受保护的独立空间(栈空间)
- 方法的局部变量是独立的,不会相互影响,比如n变量
- 如果方法中使用的是引用数据变量(比如数组,对象),就会共享该引用类型的数据
- 递归必须向退出递归的条件逼近,否则就是无限递归,出现StrackOverflowError,死归了
- 当一个方法执行完毕时,同时当方法执行完毕或者返回时,该方法也执行完毕
课堂练习
- 请使用递归的方式求出斐波那契数1,1,2,3,5,8,13…给你一个整数n,求出它的值是多少
- 猴子吃桃子问题:有一堆桃子,猴子第一天吃了其中的一半,并再多吃了一个!以后每天猴子都吃其中的一半,然后再多吃一个。当到第10天时,想再吃时(即还没吃)发现只有1个桃子了。问题:最初共多少个桃子?
import java.util.Scanner;
public class RecursionExercise01 {
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("请输入一个整数");
TT t1=new TT();
Scanner input=new Scanner(System.in);
// long n=input.nextInt();
// System.out.println("当n="+n+"时对应的斐波那契数是"+t1.fibonacci(n));
int day;
day=input.nextInt();
System.out.println("第"+day+"天有"+t1.peach(day)+"个桃子");
}
}
class TT{
/*
请使用递归的方式求出斐波那契数1,1,2,3,5,8,13...给你一个整数n
思路分析
1.当n=1时,斐波那契数是1
2.当n=2时,斐波那契数是1
3.当n>=3 斐波那契数 是前两个数的和
4.这里就是一个递归的思路
*/
public int fibonacci(long n) {
if(n>=1){
if(n==1||n==2) {
return 1;
}else {
return fibonacci(n-1)+fibonacci(n-2);
}
}else{
System.out.println("要求输入的n>=1的整数");
}
return -1;
}
/*
猴子吃桃子问题:有一堆桃子,猴子第一天吃了其中的一半,并再多吃了一个!
以后每天猴子都吃其中的一半,然后再多吃一个。当到第10天时,
想再吃时(即还没吃),发现只有一个桃子了。问题:最初共有多少个桃子
思路分析 逆推
1.day=10 时有1个桃子
2.day=9 时有(day10+1)*2=4
3.day=8 时有(day9+1)*2=10
4.规律就是 前一天的桃子 =(后一天的桃子 +1)*2
5.递归
*/
public int peach(int day) {
if(day==10) { //第10天,只有一个桃
return 1;
}else if(day>=1&&day<=9){
return(peach(day+1)+1)*2;
}else {
System.out.println("day在1-10,请重新输入");
return -1;
}
}
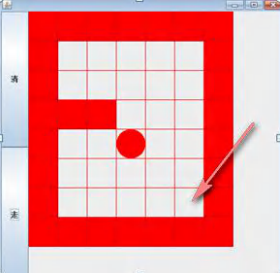
}递归调用实例-迷宫问题
public class MiGong {
//编写一个 main 方法
public static void main(String[] args) {
//思路
//1. 先创建迷宫,用二维数组表示 int[][] map = new int[8][7];
//2. 先规定 map 数组的元素值: 0 表示可以走 1 表示障碍物
int[][] map = new int[8][7];
//3. 将最上面的一行和最下面的一行,全部设置为 1
for(int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
//4.将最右面的一列和最左面的一列,全部设置为 1
for(int i = 0; i < 8;i++){
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
map[2][2] = 1; //测试回溯
// map[2][1] = 1;
// map[2][2] = 1;
// map[1][2] = 1
//输出当前的地图
System.out.println("=====当前地图情况======");
for(int i = 0; i < map.length; i++) {
for(int j = 0; j < map[i].length; j++) {
System.out.print(map[i][j] + " ");//输出一行
}
System.out.println();
}
//使用 findWay 给老鼠找路
T t1 = new T();
//下右上左
t1.findWay(map, 1, 1);
System.out.println("\n====找路的情况如下=====");
for(int i = 0; i < map.length; i++) {
for(int j = 0; j < map[i].length; j++) {
System.out.print(map[i][j] + " ");//输出一行
}
System.out.println();
}
}
}
class T {
//使用递归回溯的思想来解决老鼠出迷宫
//解读
//1. findWay 方法就是专门来找出迷宫的路径
//2. 如果找到,就返回 true ,否则返回 false
//3. map 就是二维数组,即表示迷宫
//4. i,j 就是老鼠的位置,初始化的位置为(1,1)
//5. 因为我们是递归的找路,所以我先规定 map 数组的各个值的含义
// 0 表示可以走 1 表示障碍物 2 表示可以走 3 表示走过,但是走不通是死路
//6. 当 map[6][5] =2 就说明找到通路,就可以结束,否则就继续找.
//7. 先确定老鼠找路策略
public boolean findWay(int[][] map , int i, int j) {
if(map[6][5] == 2) {//说明已经找到
return true;
} else {
if(map[i][j] == 0) {//当前这个位置 0,说明表示可以走
//我们假定可以走通
map[i][j] = 2;
//使用找路策略,来确定该位置是否真的可以走通
//下->右->上->左
if(findWay(map, i + 1, j)) {//先走下
return true;
} else if(findWay(map, i, j + 1)){//右
return true;
} else if(findWay(map, i-1, j)) {//上
return true;
} else if(findWay(map, i, j-1)){//左
return true;
} else {
map[i][j] = 3;
return false;
}
} else { //map[i][j] = 1 , 2, 3
return false;
}
}
}
//修改找路策略,看看路径是否有变化
//下->右->上->左 ==> 上->右->下
public boolean findWay2(int[][] map , int i, int j) {
if(map[6][5] == 2) {//说明已经找到
return true;
} else {
if(map[i][j] == 0) {//当前这个位置 0,说明表示可以走
//我们假定可以走通
map[i][j] = 2;
//使用找路策略,来确定该位置是否真的可以走通
//上->右->下->左
if(findWay2(map, i - 1, j)) {//先走上
return true;
} else if(findWay2(map, i, j + 1)){//右
return true;
} else if(findWay2(map, i+1, j)) {//下
return true;
} else if(findWay2(map, i, j-1)){//左
return true;
} else {
map[i][j] = 3;
return false;
}
} else { //map[i][j] = 1
return false;
}
}
}
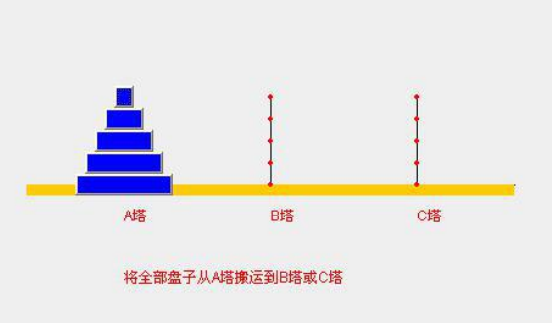
}递归调用实例-汉诺塔
- 汉诺塔传说
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着 64 片圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
假如每秒钟移动一次,共需多长时间呢?移完这些金片需要 5845.54 亿年以上,太阳系的预期寿命据说也就是数百亿年。真的过了 5845.54 亿年,地球上的一切生命,连同梵塔、庙宇等,都早已经灰飞烟灭
- 汉诺塔代码实现
import java.util.Scanner;
public class HanoiTower {
public static void main(String[] args) {
// TODO Auto-generated method stub
Tower tower=new Tower();
System.out.println("请输入汉诺塔上面要移动的盘子数");
Scanner n1=new Scanner(System.in);
int n=n1.nextInt();
tower.move(n,'A','B','C');
}
}
class Tower{
//方法
//num表示要移动的个数,a,b,c分别表示A塔,B塔,C塔
public void move(int num,char a,char b,char c) {
//如果只有一个盘num=1
if(num==1) {
System.out.println(a+"->"+c);
}else {
//如果有多个盘,可以看成两个,最下面的和上面的所有盘(num-1)
//(1)先移动a上面的n-1个盘到b,借助c
move(num-1,a,c,b);
//(2)把a最下面的这个盘,移动到c
System.out.println(a+"->"+c);
//(3)再把b上的n-1个盘,移动到c,借助a
move(num-1,b,a,c);
}
}
}


